Казино Азино777 предлагает играть на реальные деньги в сотни качественных онлайн автоматов после регистрации. Официальный сайт Azino777 и рабочее зеркало www.lazer777.ru доступны круглосуточно, 24\7. При входе с мобильного устройства предлагается перейти в мобильную версию — Azinomobile, которую можно скачать или играть онлайн.
Основная часть ассортимента игр Azino777 — это различные варианты гаминаторов. Book of Ra, Fruit Machine, Deluxe Luxor и многие другие. Как старые (выпущенные ещё в 2005 годах), так и современные версии.
Содержание:
| Основная информация: | |
| 🌍Официальный сайт | www.lazer777.ru |
| 🎁Бонус | 100% на депозит. |
| 🚀Год основания | 2011 |
| 💵Валюта счета | Российский рубль , Доллар |
| 💳Способы депозита | Visa , MasterCard , Qiwi , Яндекс.Деньги , WebMoney , Liqpay , Alfa-Click |
| 💰Способы вывода | Visa , MasterCard , Qiwi , Яндекс.Деньги , WebMoney |
| 🌐Язык | Русский, Английский |
| 🏦Лицензия | ✅ Да |
| 🎰Софт | Endorphina, Belatra, Betsoftgaming, Ezugi, SoftSwiss, Habanero, Amatic, Pragmatic Play и др. |
| 🚫Запрещенные страны | США |
Казино Azino777 Casino регистрация и вход
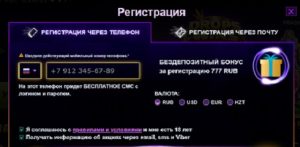
Регистрация в Azino777 предполагает выполнение таких действий:
- Нажать на кнопку «Регистрация»
- Выбрать стандартный или альтернативный вариант регистрации — заполнить анкету или создать учетную запись с использованием аккаунта в Mail.ru, Google+, Yandex, Facebook, Twitter, Vk, Ok
При выборе стандартного способа нужно заполнить все поля анкеты с красной пометкой:
- Имейл и пароль
- Имя, фамилия
- Страна проживания
- Дата рождения
- Номер телефона
- Валюта игрового счета
Регистрироваться можно лицам в возрасте 18+
Администрация требует обязательного подтверждения об ознакомлении с правилами и условиями онлайн-казино, а также своего совершеннолетия. За регистрацию новый клиент получит фриспины, фрибет или бонусы — выбор подарка зависит от его желания.
Форма для входа в казино выглядит так:
Официальный сайт
Азино777 – одно из лучших оффшорных онлайн-казино. Здесь доступно огромное количество разнообразных игровых автоматов, настольные игры с реальным крупье, несколько вариантов лотерей.
Бонусная программа ориентирована на начинающих и продолжающих игроков. Вся информация доступна на официальном сайте, войти на который можно через рабочее зеркало на сегодня. Увеличить депозит можно, принимая участие в турнирах.
Официальный сайт Azino777 отличается от многих российских онлайн-казино. Игровой ресурс отличается лаконичным дизайном, отсутствием ярких баннеров, всплывающих блоков и рекламных предложений. Стартовая страница оформлена в темном фоне, на котором броско смотрится логотип казино.
Игроки могут самостоятельно выбрать формат официального сайта. Пользователи, у которых есть возможность играть через полную версию для ПК остаются здесь. Остальные геймеры могут перейти в мобильную версию и запускать слоты со смартфона.
Дополнительно разработана удобная клиент-программа для мобильных устройств на операционных системах Андройд и ИОС. Скачать их можно с сайта Азино 777, кликнув на иконку с соответствующим логотипом ОС.
Основные преимущества и недостатки официального сайта:
| a | — | 2 |
| p | + | 10 |
Преимущества клуба:
- Разнообразный выбор игровых автоматов;
- Щедрая бонусная программа;
- Различные турниры и розыгрыши;
- Удобная навигация по разделам сайта.
Рабочее зеркало

Если игроки не могут попасть на официальный сайт Азино 777, они прибегают к посещению рабочего на сегодня зеркала. В каждом случае в Azino777 их ждет множество популярных развлечений. Можно сыграть в слоты, рулетку, карты, а в букмекерской конторе клиенты делают ставки на разные виды спорта.
| azino777.com | azinomobile.net | azino777.ru |
| azino.online | kazino777.vip | azino888.com |
Чтобы узнать, какие зеркала рабочие именно сегодня, пользователь может:
- добавить дополнительные домены в закладки браузера (все актуальные адреса находятся на официальном сайте в разделе «Помощь»);
- подписаться на официальный Телеграм-канал (там выкладывают все новости заведения, а также перечень рабочих зеркал);
- подписаться на e-mail рассылку (для зарегистрированных пользователей, в случае запрета доступа к сайту автоматически всем гемблерам рассылают письма с перечнем рабочих зеркал).
Ещё вариант — это использовать мобильное приложение Azino mobile для Android-смартфонов. Там уже предустановлены все зеркала, обновляются автоматически каждый день. Если к основному серверу не удается подключиться, то приложение поочередно отправляет запросы зеркалам.
Следует учесть, что их обновляют еженедельно. Поэтому список закладок в браузере рекомендуется периодически обновлять.
Ввод и вывод средств
Клуб Азино 777 принимает рубли, доллары, евро и другие валюты. Для вывода денег можно выбрать любой из доступных способов.
Чтобы вывести деньги с казино на карту, нужно пройти верификацию. Игроку нужно предоставить в саппорт фото паспорта и банковской карты.
Процесс вывода денег простой:
- зайти в раздел «Касса» в личном кабинете на официальном сайте или зеркале Джойказино;
- нажать вкладку «Получить выигрыш» и выбрать в списке способ (вывести деньги можно через сервис, который хотя бы один раз использовался для пополнения депозита);
- указать сумму и нажать на кнопку «Получить выигрыш».
| Платежная система | Минимальный депозит |
| Банковские карты MasterCard, Visa, Maestro | 2000RUB |
| Qiwi | 500 RUB |
| WebMoney | нет |
| Яндекс. Деньги | 500 RUB |
| ИнтерКасса | 1000 RUB |
| Bitcoin | 500 RUB |
| Neteller | 700 RUB |
| Skrill | 700 RUB |
| PayAnyWay | 700 RUB |
| PerfectMoney | 500 RUB |
| SMS | Не более 5 сообщений в течение 5 минут |
| Мобильный платеж | 500 RUB |
Перед подачей заявки стоит учесть, что в Azino777 Casino не допускается использование чужих карт для ввода и вывода средств. При нарушении данного правила администрация имеет право конфисковать деньги с аккаунта и аннулировать выигрыши.
Бонусы и Привилегии
Одно из самых популярных казино на русскоязычном рынке Azino 777 предлагает каждому новому игроку воспользоваться бездепозитным бонусом за регистрацию и получить до 777 рублей без депозита.
| 777 | + | — |
| бездеп | с выводом | при регистрации только с телефона |
Для получения бездепа нужно:
- Зарегистрироваться в соответствии с правилами онлайн-казино.
- Зарегистрироваться с мобильного телефона.
Для получения бонуса за регистрацию, обязательно проходите регистрацию по номеру мобильного телефона! Если зарегистрируетесь по e-mail, бонус начислен не будет!
Техподдержка
- Юридический адрес: P.O. Box 3075, Curacao, Willemstad, Heelsumstraat 51 E-Commerce Park
- Контакты в России: 8 800 333 24 39
- support@azino777.com



Раньше я думал, что играть в казино это плохо. Потом увидел, что многие мои знакомые на работе играют. Я заинтересовался этой темой и они мне все объяснили. Я легко зарегистрировался в этом казино и теперь играю почти каждый вечер. Для меня это лучший отдых и денег я почти не трачу, а наоборот выигрываю. Тут столько бонусов, что можно даже свои деньги не вводить.
Хорошее казино. На сайте очень много автоматов на любой вкус. Именно здесь можно играть в любимые игры и при этом неплохо зарабатывать. Azino777 стабильно выплачивает выигрыш уже не один год.
Участвую практически во всех активностях казино. Акции, турниры, программа лояльности. В большинстве случаев условия выгодные, не сложно выполнить требования, призы хорошие. Думаю, здесь самое место, если не хотите много денег тратить.
Нашел себе довольно прибыльное развлечение на сайте казино 777. Такое количество щедрых автоматов я не видел более нигде. Играть легко и удобно. Ставки на любой вкус, а коэффициенты очень радуют и вдохновляют. Качественное казино, проверенное, надежное. Да и как гарантия стабильной работы- наличие лицензии. А с ней не побалуешь, мигом вылетишь с верхних строчек топ-казино.